14. F-beta Score
F-beta Score
09 Quiz Fbeta Score SC V1
Quiz
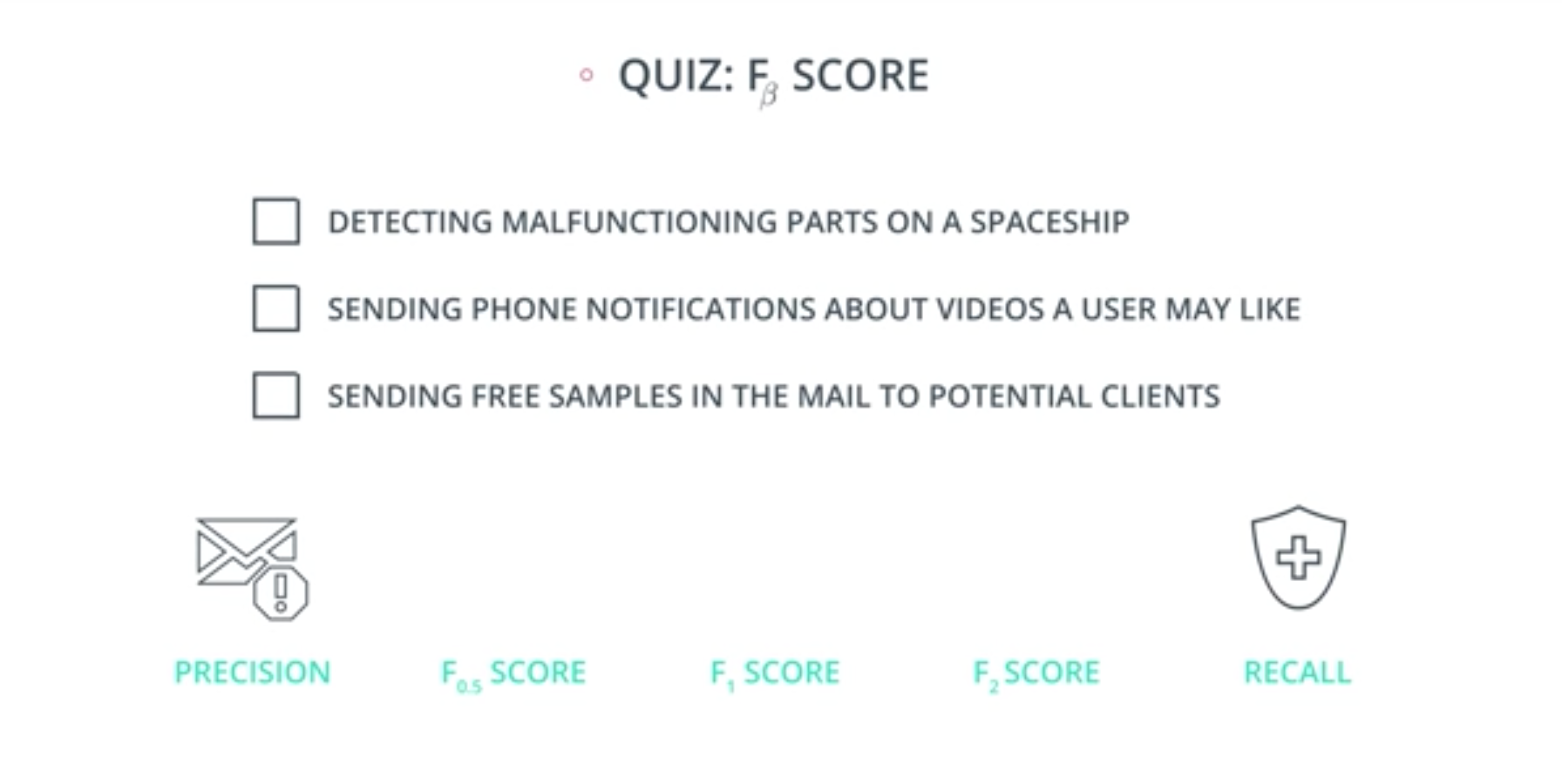
F-beta Score Quiz
QUIZ QUESTION::
Out of the following three models, which one should have an F-beta score of 2, 1, and 0.5? Match each model with its corresponding score.
- Detecting malfunctioning parts in a spaceship
- Sending phone notifications about videos a user may like
- Sending promotional material in the mail to potential clients
ANSWER CHOICES:
|
Model |
F-beta Score |
|---|---|
Spaceship |
|
Notifications |
|
Promotional Material |
SOLUTION:
|
Model |
F-beta Score |
|---|---|
|
Notifications |
|
|
Spaceship |
|
|
Promotional Material |
Boundaries in the F-beta score
Note that in the formula for
F_\beta
score, if we set
\beta = 0,
we get
F_0 = (1+0^2) \cdot \frac{\text{Precision} \cdot \text{Recall}}{0 \cdot \text{Precision} + \text{Recall}} = \frac{\text{Precision} \cdot \text{Recall}}{\text{Recall}} = \text{Precision}.
Therefore, the minimum value of
\beta
is zero, and at this value, we get the precision.
Now, notice that if N is really large, then
F_\beta = (1+N^2) \cdot \frac{\text{Precision} \cdot \text{Recall}}{N^2 \cdot \text{Precision} + \text{Recall}} = \frac{\text{Precision} \cdot \text{Recall}}{\frac{N^2}{1+N^2}\text{Precision} + \frac{1}{1+N^2}\text{Recall}}.
As
N
goes to infinity, we can see that
\frac{1}{1+N^2}
goes to zero, and
\frac{N^2}{1+N^2}
goes to 1.
Therefore, if we take the limit, we have
{\lim_{N\rightarrow \infty}} F_N = \frac{\text{Precision} \cdot \text{Recall}}{1 \cdot \text{Precision} + 0 \cdot \text{Recall}} = \text{Recall}.
Thus, to conclude, the boundaries of beta are between 0 and
\infty.
- If
\beta = 0,
then we get precision. - If
\beta = \infty,
then we get recall. - For other values of
\beta,
if they are close to 0, we get something close to precision, if they are large numbers, then we get something close to recall, and if
\beta = 1,
then we get the harmonic mean of precision and recall.